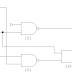
Half Adder using NAND gate only
What this suggests is also intuitively logical: we can use two half-adder circuits. The first will add A and B to produce a partial Sum, while the second will add CIN to that Sum to produce the final S output. If either half-adder produces a carry, there will be an output carry. Thus, COUT will be an OR function of the half-adder Carry outputs. The resulting full adder circuit is shown here ( fig 3.2).,,,,,,,,,,,,,,,,

———————————————————————————
Full Adder using NAND gate only
To construct a full adder circuit, we’ll
need three inputs and two outputs. Since we’ll have both an input carry
and an output carry, we’ll designate them as CIN and COUT. At the same time, we’ll use S to designate the final Sum output. The resulting truth table is shown to the right.
Hmmm. This is looking a bit messy. It looks as if COUT may
be either an AND or an OR function, depending on the value of A, and S
is either an XOR or an XNOR, again depending on the value of A. Looking a
little more closely, however, we can note that the S output is actually
an XOR between the A input and the half-adder SUM output with B and CIN inputs. Also, the output carry will be true if any two or all three inputs are logic 1.What this suggests is also intuitively logical: we can use two half-adder circuits. The first will add A and B to produce a partial Sum, while the second will add CIN to that Sum to produce the final S output. If either half-adder produces a carry, there will be an output carry. Thus, COUT will be an OR function of the half-adder Carry outputs. The resulting full adder circuit is shown here ( fig 3.2).,,,,,,,,,,,,,,,,
fig 3.2
Truth Table
| INPUTS | OUTPUTS | |||
|---|---|---|---|---|
| A | B | CIN | COUT | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Must Share and show your lovefig 3.3Using only NAND gates
Share this on your favourite network











0 comments :
Post a Comment